数据拟合

​ 当遇到一个对于多个变量需要探求其中内在联系的问题，可以使用插值拟合方法，并通过绘图观察出潜在关系

拟合即为将数据转化为近似的曲线

例：

拟合命令如下：

%polyfit(X,Y,N) 多项式拟合，返回降幂排列的多项式系数
%polyval(P,xi) 计算多项式的值
x=[1 2 3 4 5 6 7 8 9];
y=[9 7 6 3 -1 2 5 7 20];
P=polyfit(x,y,3);
xi=0:.2:10;%生成以零点二为间隔，从0一直到10的矢量
yi=polyval(P,xi);
plot(xi,yi,x,y,'r*');

结果

曲线拟合与函数逼近

​ 曲线拟合是指已知一组离散数据，选择一个较为简单的函数f(x)（如多项式），在一定准则(如最小二乘准则)下，最接近这些数据。

​ 而曲线逼近是指已知一个较为复杂的连续函数，要求选择一个较为简单的函数，在一定准则下最接近y(x)，为函数逼近

三次样条插值函数

​ Matlab中三次样条插值有以下函数：

y=interp1(x0,y0,x,'spline');
y=spline(x0,y0,x);
pp=csape(x0,y0,conds);
pp=csape(x0,y0,conds,valconds);y=fnval(pp,x);
%x0,y0是已知数据点，x是插值点，y是插值点的函数值

对于三次样条插值，提倡使用函数csape,其返回值是pp形式

评价类模型

层次分析法

​ 最基础的模型之一，主要用于解决评价类问题，比如哪种方案更好或者哪位运动员或者员工的表现最优秀

​ 对对象的各种指标进行打分，即分配权重，最后各个指标的权重和为1

​ 用打分法解决评价类问题，可以用以下表格的思维解决

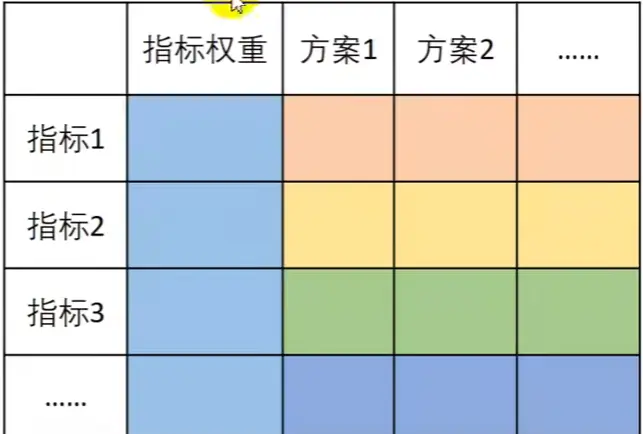
关键：

​ 1.确定评价指标

​ 2.形成评价体系

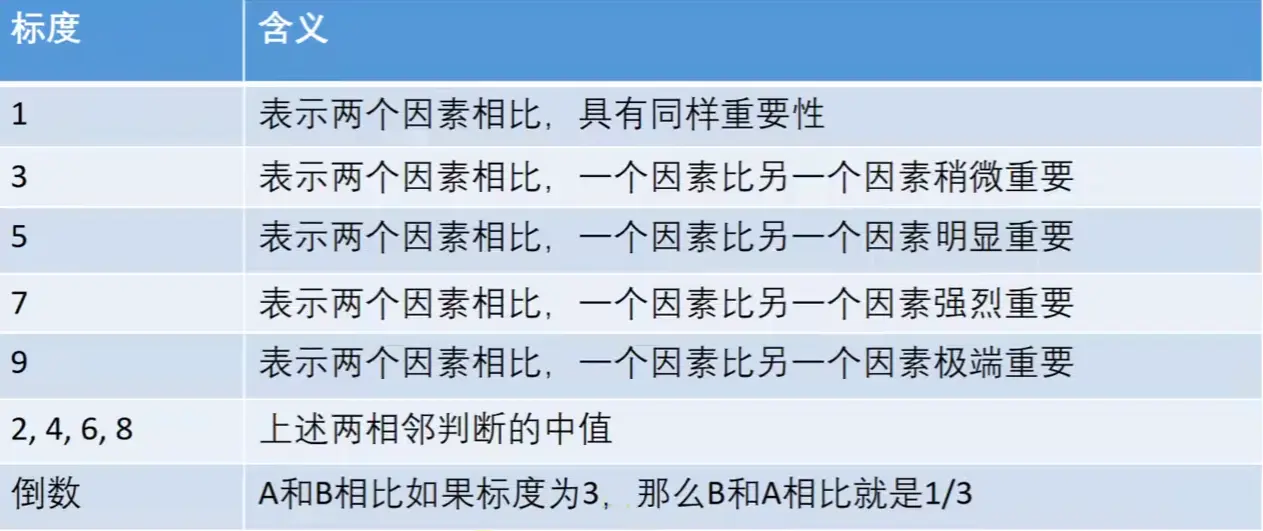
在对各种指标进行比较的时候，如果一次性考虑五个指标之间的关系，往往考虑不周，所以我们采取分而治之的思想，对所有指标两两比较，最后推算出权重

对于景点，我们有以下几个指标可以作为认为这个景点是否值得去的依据

• 景色
• 花费
• 居住
• 饮食
• 交通

随之我们也可以排出这样的一副表

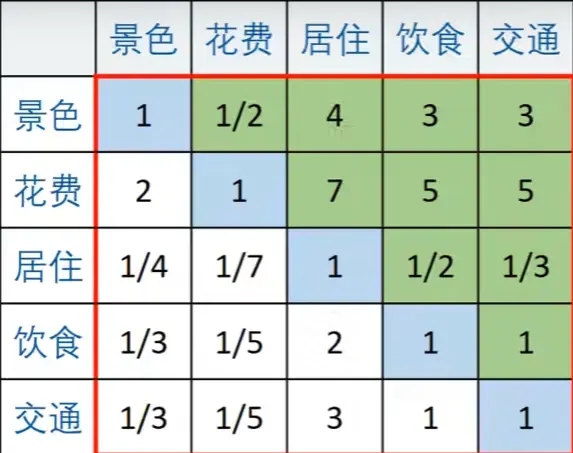
总结：可以看出上方两两因素的比较可以构成一个5*5方阵，记为A，对应的元素为aij

1. aij表示的意义是，与指标j相比，i的重要程度
2. 当i=j时，两个指标相同，因此同等重要记为1，这就解释了主对角线元素为1
3. aij>0且满足aij*aji=1(满足这一条件的矩阵为正互反矩阵)

然而，在各种指标的评价中，需要遵守最起码的原则，不然会出现不一致的现象

符合基本规律即满足aij*ajk=aik，我们称其为一致矩阵，而想要观察是否为一致矩阵，只需要看相邻两行是否成倍数关系

检验一致性：

1.计算一致性指标CI

​

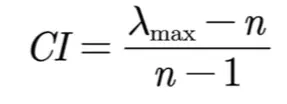
2.查找对应的平均随机一致性指标RI

3.计算一致性比例CR

在准备工作做好后，我们可以利用判断矩阵计算权重

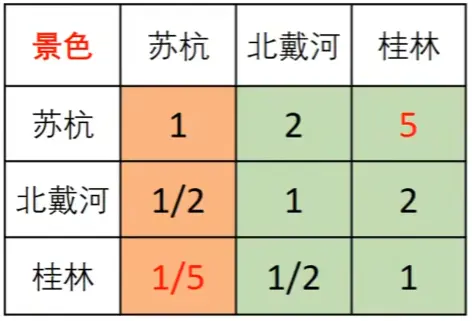
使用第一列数据，可以计算出权重

苏杭=1/（1+0.5+0.2）=0.5882

北戴河=0.5/（1+0.5+0.2)=0.2941

桂林=0.2/（1+0.5+0.2）=0.1177

以此类推，也可以通过后两列的数据计算出权重来

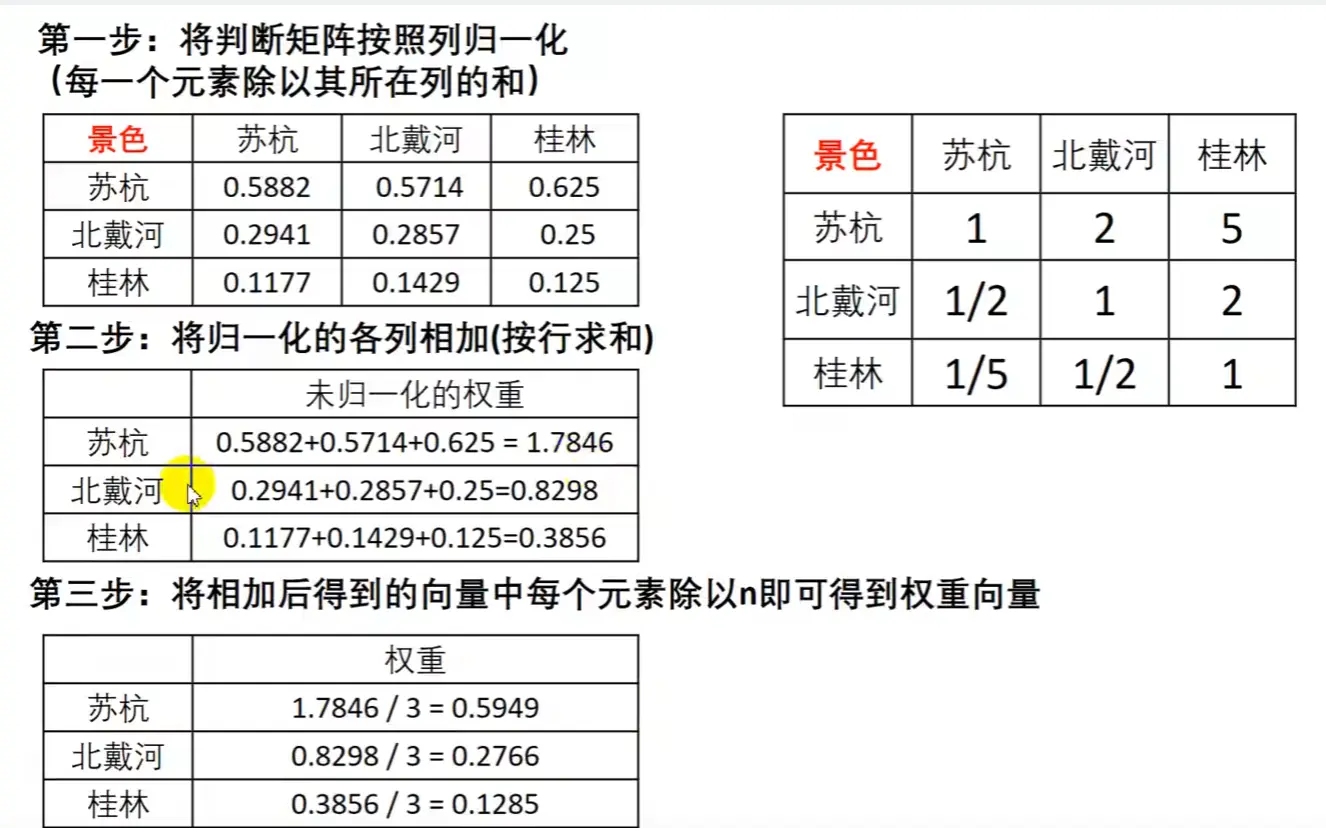
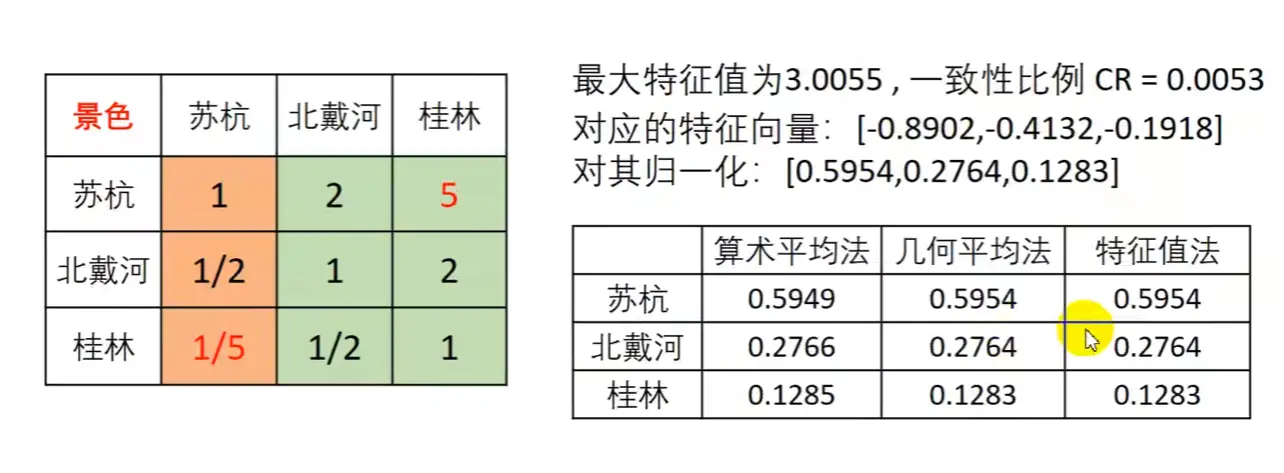
特征值法求权重

​ 如果我们的判断矩阵一致性可以接受，那么我们可以仿照一致矩阵权重的求法

1.求出矩阵A的最大特征值以及其对应的特征向量

2.对求出的特征向量进行归一化即可得到我们的权重

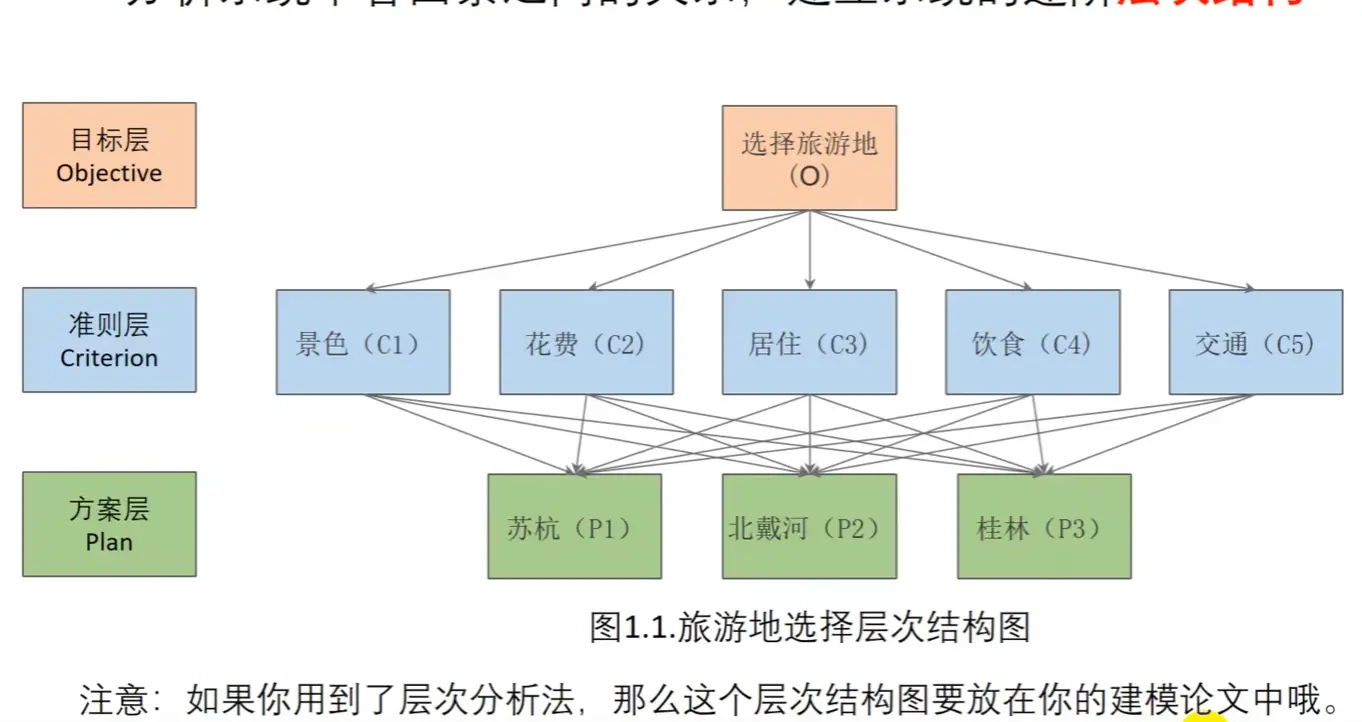
如果用到了层次分析法，那我们需要构造层次分析图，并且绘制好后放入论文中

缺点：任何评价类模型都具有主观性

线性规划模型

线性规划就是在一组线性约束条件下，求线性目标函数的最大或最小值

线性规划适用题型

​ 比如题目中提到“怎样安排/分配” “尽量多(少)” “利润最大”等词

“有什么条件，原材料等等，怎样安排利润收益最大”诸如此类

• 生产安排
• 投资收益
• 销售运输
• 车辆安排

代码实现

​ matlab中有自带的线性规划函数，Linprog函数，

首先要将其模型化为matlab标准型：目标函数最小值、约束条件小于等于号或等号

p.s:如果是求最大值比如求W的最大值，只需转化为求-W的最小值即可，约束条件的转化同理

转化案例

注意事项

f=[-40;-30];%目标函数中变量的系数矩阵
A=[1,1;
-1,0;
0,-1;
240,120];%小于等于的约束条件中系数矩阵
b=[6;-1;-1;1200];%小于等于的约束条件中常数项矩阵

Linprog函数

​ 对于在线性规划中使用的核心函数，以及在后面其他类型问题中需要使用的方法，对于linprog函数，需要作出详细的使用方法

同样的，我们先引入一个例题，来更好的理解该函数的用法

%matlab中linprog函数的标准形式为
%[x,fval]=linprog(f,A,b,Aeq,beq,lb,ub)
%f为价值向量
f=[-2;-3;5];
%a为不等式约束
a=[-2,5,-1;
	1,3,1];
%b为不等式约束的值
b=[-10;12];
%aeq为线性等式约束
aeq=[1,1,1];
%beq同理
beq=7;
[x,y]=linprog(f,a,b,aeq,beq,zeros(3,1));
x,y=-y;
%zeros()函数的意思是，构造一个3行1列的全0矩阵

运行结果

>> f=[-40;-30];
>> a=[1,1;-1,0;0,-1;240,120];
>> b=[6;-1;-1;1200];
>> [x,y]=linprog(f,a,b)

x =

    4.0000
    2.0000


y =

 -220.0000

>> y=-y

y =

  220.0000

可转化为线性规划的问题

​ 有的问题看起来不是数学规划问题，但是实际上也可以变化成线性规划的问题来解决

比如数学规划问题

我们再次举出一个例子

对于这种非典型的线性规划问题，对于他来说matlab的标准式有一些区别

即对于最后调用函数时，参数的设置与典型的线性规划有一些区别

c=1:4;c=[c,c];
a=[1,-1,-1,1;1,-1,1,-3;1,-1,-2,3];
a=[a,-a];%构造变换后新的系数矩阵
b=[-2 -1 -1/2];
[y,z]=linprog(c,a,b,[],[],zeros(8,1))%此处没有等式约束，所以对应矩阵为空矩阵
x=y(1:4)-y(5:end)%变换到原问题的解，x=u-v

整数规划

​ 整数规划是什么？

数学规划中的变量（部分或全部）限制为整数时，称为整数规划

举一个将线性规划的问题转化为整数规划后的情况

对于整数规划，求解方法有如下分类

1. 分支定界法
2. 割平面法
3. 隐枚举法
   1. 过滤隐枚举法
   2. 分支隐枚举法
4. 匈牙利法
5. 蒙特卡洛法

0-1型整数规划

​ 0-1型整数规划指的是问题中的变量x仅取值0或1

​ 举一个例子，运送货物，有两种运输方式可供选择，但只能选择一种运输方式：1.用车运输 2.用船运输

用车运输时，约束条件为：

5x1+4x2<=24

用船运输时，约束条件为：

7x1+3x2<=45

为了统一一个问题，引入0-1变量：

则对于0-1型整数规划问题，我们可将该问题的约束条件改写为

​ 其中M为充分大的数

当问题中有多个互相排斥的约束条件时，我们的应对也很简单，引入m个0-1变量即可

Yi=1时，第i个约束起作用，等于0时，则第i个约束不起作用

关于固定费用的问题(Fixed Cost Problem)

​ 线性规划中，有些问题要求使成本最小，那么可设固定成本为常数，并且在线性规划的模型中不必明显列出，但有些问题不能用一般线性规划描述，可改变为混合整数规划来解决

​ 现在假设有这样一个情景，生产一批货物，有三种方式，每一种不同的方式带来的单件成本和产量以及固定成本不一样

那对于这类问题，我们可以这样入手并且得到目标函数

对于其中的各个变量，我们有以下不同的限制

于是我们可以对总成本构造相应的目标函数：

min z=(k1y1+c1x1)+(k2y2+c2x2)+(k3y3+c3y3)

蒙特卡洛法(随机取样法)

​ 蒙特卡洛法，基于大量事件的统计结果来实现一些确定性问题的计算

​ 使用蒙特卡洛法生成相关分布的随机数

设计的随机试验的思想：在矩形区域[0,12]*[0,9]上产生均匀分布的10的七次方个随机点，统计随机点落在曲边三角形的频数，则曲边三角形的面积近似为上述举行的面积乘以频率

Matlab程序如下

clc,clear
x=unifrnd(0,12,[1,10000000]);
y=unifrnd(0,9,[1,10000000]);
pinshu=sum(y<x.^2&x<=3)+sum(y<12-x&x>=3);
area_appr=12*9*pinshu/10^7;

非线性整数规划当自变量维数很大和取值范围很宽时，穷举法是不现实的，但是采用蒙特卡洛法可以得出一个满意解

首先编写M文件mente.m定义目标函数f和约束向量函数g

function[f,g]=mente(x);
f=x(1)^2+x(2)^2+3*x(3)^2+4*x(4)^2+2*x(5)^2-8*x(1)-2*x(2)-3*x(3)-x(4)-2x(5);
x(4)-2*x(5);
g=[sum(x)-400
x(1)+2*x(2)+2*x(3)+x(4)+6*x(5)-800
2*x(1)+x(2)+6*x(3)-200
x(3)+x(4)+5*x(5)-200]
%该文件与上方约束条件为对应关系，一目了然

然后编写程序求解

rand('state',sum(clock));%初始化随机数发生器
p0=0;
tic %计时开始
for i=1:10^6
	x=randi([0,99],1,5);%产生一行五列的区间[0，99]上的随机整数
	[f,g]=mengte(x);
	if all(g<=0)
			if p0<f
				x0=x;p0=f;%记录下当前较好的解
				end
		end
	end
	x0,p0
	toc%计时结束
%由于是随机模拟，因此每次运行的结果都是不一样的

整数线性规划的计算机求解

Matlab求解混合整数线性规划的命令为

[x,fval]=intlinprog(f,intcon,A,b,Aeq,beq,lb,ub)

MATLAB标准式：

非线性规划

理解非线性规划其实很简单

• 线性规划:所有变量都是一次方
• 非线性规划:至少一个变量不是一次方

对于该函数中的fun1和fun2参数，应当在新建的文件中另外书写

fun1

function f=fun1(x)%后面的函数名一定要和文件名相同，func2同理
f=sum(x.^2)+8;

fun2

function [g,h]=func2(x)
g=[-x(1)^2+x(2)-x(3)^2
   x(1)+x(2)^2+x(3)^3-20]
h=[-x(1)-x(2)^2+2
   x(2)+2*x(3)^2-3]

test_of_func

[x,y]=fmincon('fun1',[10;0;0],[],[],[],[],[0;0;0],[],'func2')

非线性规划适用的典型赛题

• 题目中提到“怎样安排/分配，尽量多/少等等”，大致条件与线性规划相同，但是变量起码有一个是非一次方
• 投资规划&投资决策：求出最佳投资方案

​ 在投资决策中，约束分为等式约束以及不等式约束

• 角度调整：飞行管理避免相撞；影院最佳视角
  • 飞机位置，速度，进入区域后判定是否相撞，飞机飞行方向角调整的幅度尽量小
  • 电影院视角仰角影响观影体验，什么位置观影最佳
  • 涉及三角函数，为非线性
• 生产安排：原材料、设备有限制、总利润最大(目标函数或约束条件含有非线性变量)

当将一个实际问题归结成非线性规划问题时，一般注意：

1. 确定供选方案：收集同问题有关的资料和数据，对问题的情况要足够熟悉
2. 提出追求目标：通过资料分析，结合实际需求，追求极小化或者极大化
3. 给出价值标准：提出追求目标后，确定考虑目标的好或者坏，并用具体的数量形式描述
4. 寻求限制条件：问题中需要考虑到实际上会有的限制条件

Matlab中非线性规划的求解命令是

[x,fval]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
%x的返回值式决策向量x的取值，fval返回的是目标函数的取值
%其中fun是用M文件定义的函数f(x)
%x0是x的初始值
%A,b,Aeq,beq定义了线性约束A*b<=b,Aeq*x=beq
%若没有线性约束，则A=[],b=[],Aeq=[],beq=[]
%lb和ub是变量x的下界和上界
%若上下界无约束，则可以写lb各分量为-inf(为负无穷)，ub各分量为inf(正无穷)
%nonlcon是用M文件定义的非线性向量函数c(x),ceq(x)
%options定义了优化参数，可以使用Matlab默认的参数配置

无约束极值问题的符号解

例

对于多元多次方程，求极值的步骤为

1. 分别对各项进行求导，得出对应的偏导数
2. 求出偏导数之后进行高阶偏导数变换

对于Hessian阵：

• 驻点处Hessian阵为正定阵，则该点取最小值
• 驻点处Hessian阵为负定阵，则该点取最大值
• 驻点处Hessian阵为不定阵，则该驻点不是极值点

MATLAB程序实现如下：

clc,clear;
syms x y
f=x^3-y^3+3*x^2+3*y^2-9*x;
df=jacobian(f);%求一阶偏导数
d2f=jacobian(df);%求Hessian阵
[xx,yy]=solve(df)%求驻点
xx=double(xx);yy=double(yy);%转化为双精度浮点型数据，下面判断特征值的正负，必须是数值型数据

for i=1:length(xx)
	a=subs(d2f,{x,y},{xx(i),yy(i)});
	b=eig(a);%求矩阵的特征值
	f=subs(f,{x,y},{xx(i),yy(i)});f=double(f);
	if all(b>0)
		fprintf('(%f,%f)是极小值点，对应的极小值为%f\n',xx(i),yy(i),f);
	elseif all(b<0)
    	fprintf('(%f,%f)是极大值点，对应的极大值为%f\n',xx(i),yy(i),f);
    elseif any(b>0)&any(b<0)
    	fprintf('(%f,%f)不是极值点\n',xx(i),yy(i));
    else
    	fprintf('无法判断(%f,%f)是否是极值点\n',xx(i),yy(i));
    	end
    end

结果

(1.000000,0.000000)是极小值点，对应的极小值为-5.000000
(-3.000000,0.000000)不是极值点
(1.000000,2.000000)不是极值点
(-3.000000,2.000000)是极大值点，对应的极大值为-5.000000

无约束极值问题的数值解

Matlab中求解无约束极小值的函数有

fminunc
fminsearch
%其使用格式分别为
[x,fval]=fminunc(fun,x0,options)
[x,fval]=fminsearch(fun,x0,opitons)
%fun-要计算最小值的函数
%x0-初始点
%options-优化选项
%problem-问题结构体
%fminsearch只能求给定的初始值附近的一个极小值点

Matlab程序如下

clc,clear
f=@(x)x(1)^3-x(2)^3+3*x(1)^2+3*x(2)^2-9*x(1);%定义匿名函数
g=@(x)-f(x);
[xy1,z1]=fminunc(f,rand(2,1))%求极小值点
[xy2,z2]=fminsearch(g,rand(2,1));%求极大值点
xy2,z2=-z2

求函数的零点和方程组的解

例：求多项式f(x)=x^3-x^2+2x-3的零点

Matlab程序如下

clc,clear
xishu=[1 -1 2 -3];%多项式是用向量定义的，系数从高次幂到低次幂
x0=roots(xishu)

符号求解程序如下

syms x
x0=solve(x^3-x^2+2*x-3)%求函数零点的符号解
x0=vpa(x0,5)%化成小数格式的数据

数值解的程序如下

y=@(x)x^3-x^2+2*x-3;
x=fsolve(y,rand)%只能求给定初始值附近的一个零点

约束极值问题

二次规划

​ 若某非线性规划的目标函数为自变量x的二次函数，约束条件又全是线性的，就称这种规划为二次规划

Matlab标准式

求解命令为

[x,fval]=quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)

返回值x是决策向量x的值

Matlab代码

h=[4,-4;-4,8];
f=[-6;-3];
a=[1,1;4,1];
b=[3;9];
[x,value]=quadprog(h,f,a,b,[],[],zeros(2,1))

结果

x =
    1.9500
    1.0500
value =
  -11.0250

罚函数法

​ 罚函数法可将非线性规划问题的求解转化为求解一系列无约束极值问题

Matlab标准式

取一个充分大的数M，然后利用如下公式构造函数

例：求解下列非线性规划

1. 定义增广目标函数，编写M函数test1.m如下

   function g=test1(x);
   M=50000;
   f=x(1)^2+x(2)^2+8;
   g=f-M*min(x(1),0)-M*min(x(2),0)-M*min(x(1)^2-x(2),0)+M*abs(-x(1)-x(2)^2+2);

2. 求增广目标函数的极小值，在matlab输入

   [x,y]=fminsearch('test1',rand(2,1))

大例题：飞行管理问题

​ 请对这个避免碰撞的飞行管理问题建立数学模型，列出计算步骤，对以下数据进行计算，要求飞机飞行方向角调整的幅度尽量小

模型一

​ 考察两架飞机i和j飞行时，可以将其中一架飞机视作不动，另一架飞机以相对速度飞行

符号解和数值解的区别

符号解（准确的叫法是解析解）是准确解，如果方程都能有解析解当然愿意用它。但事实上很多常微分方程是没有解析解的，因此只能能过数值的方法去解决。

多目标规划

如何判定题目要使用多目标规划，只需抓住一句关键语句：既要XXX，又要XXX

线性规划都是一个目标函数，例如工业生产两种产品，追求最大化利润

但是现在有多个目标需要满足时，问题就成为了多目标规划问题

在题干中，有一些词条可以注意：

• 不超过:尽量“<=”
• 充分利用:尽量“=”
• 不少于:尽量“>=”

在多目标规划中同时有多个目标需要满足时，需要衡量每个目标的完成情况，并在主观上区分三个目标的重要性，使得整体的完成情况尽量好

如何衡量每个目标的完成情况？

​ 正负偏差变量

正偏差变量超了也不怕，但是负偏差变量是越小越好

绝对约束

​ 是模型中自带的约束条件，必须满足，否则是不可行解

目标约束

​ 模型中对不等式有段追求的值允许有偏差

那么，在问题解决过程中，我们需要在主观上区分多个目标的重要性，使得整体的完成情况尽量好，为此我们引入了优先因子的概念

优先因子

可以进行查阅相关论文，也可自己主观判断

在对多目标规划问题进行了具体的模型建立之后，我们就需要将其具象化到代码之中，MATLAB中的求解方法即为使用fgoalattain函数

首先我们先总结出问题的具体约束

图与网络模型及方法

​ 直观的讲，对于平面上的n个点，把其中的一些点对用曲线或直线连接起来，不考虑点的位置与连线曲直长短，这样形成的一个关系结构就是一个图。记作G=(V,E),V是以上述点为元素的顶点集，E是以上述连线为元素的边集
​ 对于图以及相邻顶点之间的关系，有两种表示方法

1. 邻接矩阵表示法：当相邻顶点之间赋权时，记Wij=权值或者0，无赋权时记作1或0
2. 稀疏矩阵表示法：稀疏矩阵的意思是零元素很多非零元素很少的矩阵

最短路径问题

​ 假设给出一个矩阵，矩阵i行j列的元素分别代表i城市到j城市的距离

%求第一个城市到其他城市的matlab程序如下
clc,clear
a=zeros(6);%邻接矩阵初始化,创建一个6*6的所有元素为0的矩阵
a(1,2)=50;a(1,4)=40;a(1,5)=25;a(1,6)=10;
a(2,3)=15;a(2,4)=20;a(2,6)=25;
a(3,4)=10;a(3,5)=20;
a(4,5)=10;a(4,6)=25;
a(5,6)=55;
a=a+a';%这一句的意思是让矩阵变为对称矩阵
a(a==0)=inf;%矩阵元素等于0说明两个城市没有连通的道路
pb(1:length(a))=0;pb(1)=1;index1=1;index2=ones(1,length(a));%此处length(a)值为6 
d(1:length(a))=inf;d(1)=0;
temp=1;%最新的P标号的顶点
while sum(pb)<length(a)%sum(pb)的意思是将pb矢量中的所有元素相加
	tb=find(pb==0);%find函数返回每一个非0元素的线性矢量，找出pb中等于零的值下标的线性向量
	d(tb)=min(d(tb),d(temp)+a(temp,tb));
	tmpb=find(d(tb)==min(d(tb)));
	temp=tb(tmpb(1));%可能有多个点同时达到最小值，只取其中的一个
	pb(temp)=1;
	index1=[index1,temp];
	temp2=find(d(index1)==d(temp)-a(temp,index1));
	index2(temp)=index1(temp2(1));
end
d,index1,index2%d为最终求解矩阵

关于对于其中元素有疑问的，以下是第一遍循环中，各个元素的具体值

>> tb=find(pb==0)
tb =
     2     3     4     5     6

>> d(tb)
ans =
   Inf   Inf   Inf   Inf   Inf

>> d(temp)
ans =
     0

>> a(temp,tb)
ans =
    50   Inf    40    25    10

>> d(tb)=min(d(tb),d(temp)+a(temp,tb))
d =
     0    50   Inf    40    25    10

>> tmpb=find(d(tb)==min(d(tb)))
tmpb =
     5

>> temp=tb(tmpb(1))
temp =
     6

>> pb(temp)=1
pb =
     1     0     0     0     0     1

>> index1=[index1,temp]
index1 =
     1     6

>> d(index1)
ans =
     0    10

>> d(temp)
ans =
    10

>> a(temp,index1)
ans =
    10   Inf

>> index2(temp)
ans =
     1

>> temp2=find(d(index1)==d(temp)-a(temp,index1))
temp2 =
     1

>> index2(temp)=index1(temp2(1))
index2 =
     1     1     1     1     1    

Prim算法求最小生成树

Matlab程序

clc;clear;
a=zeros(7);
a(1,2)=50;a(1,3)=60;
a(2,4)=65;a(2,5)=40;
a(3,4)=52;a(3,7)=45;
a(4,5)=50;a(4,6)=30;a(4,7)=42;
a(5,6)=70;
a=a+a';a(a==0)=inf;
result=[];p=1;tb=2:length(a);
while size(result,2)~=length(a)-1
	temp=a(p,tb);temp=temp(:);
	d=min(temp);
	[jb,kb]=find(a(p,tb)==d,1);%找第1个最小值
	j=p(jb);k=tb(kb);
	result=[result,[j;k;d]];p=[p,k];tb(find(tb==k))=[];
end
result

Kruskal算法求最小生成树

Kruskal算法的核心思想，既是在将所有的边以及所有的点分为两个集合，每一次选取一条权值最小的边，直到没有未连接入路径中的点为止

Matlab代码样例

clc;clear;
a(1,[2,3])=[50,60];a(2,[4,5])=[65,40];
a(3,[4,7])=[52,45];a(4,[5,6])=[50,30];
a(4,7)=42;a(5,6)=70;
[i,j,b]=find(a);
data=[i',j',b'];index=data(1:2,:);
loop=length(a)-1;
result=[];
while length(result)<loop
	temp=min(data(3,:));
	flag=find(data(3,:)==temp);
	flag=flag(1);
	v1=index(1,flag);v2=index(2,flag);
	if v1~=v2
		result=[result,data(:,flag)];
	end
	index(find(index==v2))=v1;
	data(:,flag)=[];
	index(:,flag)=[];
end
result

网络最大流问题

​ 网络既是一个有向图中，对于其中的每一条弧（也可叫做边），他们都有各自的一个承载量（非权值），记作C(vi,vj)>=0,称作弧的容量，同时对于每一条边，也有f(vi,vj)，称为{vi,vj}上的流量

P.s 弧是有方向的

可行流

​ 当一个流满足以下条件时，可称之为可行流

1. 对每一弧，都有0<=f(vi,vj)<=c(vi,vj)
2. 同时中间的流也满足上列条件

可行流总是存在的

最大流问题可写为如下线性规划模型