不同数据范围下，代码的时间复杂度和算法该如何选择：

n≤30, 指数级别, dfs+剪枝，状态压缩dp
n≤100 => O(n3)，floyd，dp，高斯消元
n≤1000 => O(n2)，O(n2logn)，dp，二分，朴素版Dijkstra、朴素版Prim、Bellman-Ford
n≤10000 => O(n∗n√)，块状链表、分块、莫队
n≤100000 => O(nlogn) => 各种sort，线段树、树状数组、set/map、heap、拓扑排序、dijkstra+heap、prim+heap、Kruskal、spfa、求凸包、求半平面交、二分、CDQ分治、整体二分、后缀数组、树链剖分、动态树
n≤1000000 => O(n), 以及常数较小的 O(nlogn)O(nlogn) 算法 => 单调队列、 hash、双指针扫描、并查集，kmp、AC自动机，常数比较小的 O(nlogn) 的做法：sort、树状数组、heap、dijkstra、spfa
n≤10000000 => O(n)，双指针扫描、kmp、AC自动机、线性筛素数
n≤109 => O(n√)，判断质数
n≤1018 => O(logn)，最大公约数，快速幂，数位DP
n≤101000 => O((logn)2)，高精度加减乘除
n≤10100000 => O(logk×loglogk)，k表示位数，高精度加减、FFT/NTT

基础算法

排序

快速排序

基本思想

在数组中选中一个坐标位置，将数组中比它大的数移动到其右边，比它小的移动到它的左边，然后通过递归的形式对其左右排序过一次的部分进行再次排序，直到左坐标与右坐标重合。

Emphasis

在数组中确定一个具体的坐标比对数，便于对左右两侧的数进行比对，同时注意数组的Index_Out_Of_Bounds下标越界问题

具体实现

Java的快速排序写法

 private static void quickSort(int[] arr, int left, int right) {
        if (left >= right) return;
   int x = arr[left + right >> 1], i = left - 1, j = right + 1;
   while (i < j) {
        do i++; while (arr[i] < x);
        do j--; while (arr[j] > x);
        if (i < j) {
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }

    quickSort(arr, left, j);
    quickSort(arr, j + 1, right);
}

c++的快速排序写法

void quicksort(int a[],int head,int tail)
{
    if(head>=tail) return;
    int i=head-1,j=tail+1;//确定左右坐标
    int pivot=a[head+tail>>1];//确定比对基准数
    while(i<j)
    {
        do i++;while(a[i]<pivot);//从左开始，若当前数比基准数小，则坐标继续向右移动
        do j--;while(a[j]>pivot);//从右开始，若当前数比基准数大，则坐标继续向左移动
        if(i<j)//检测左右坐标是否符合条件
        {//交换两坐标所在的数
            int temp=a[i];
            a[i]=a[j];
            a[j]=temp;
        }
    }
    quicksort(a,head,j);//递归处理前半部分
    quicksort(a,j+1,tail);//递归处理后半部分
}

拓展题目

第k个数:https://www.acwing.com/activity/content/problem/content/820/

归并排序

基本思想

将排序的整个问题分为一个个小数组的排序问题，通过从一个个局部入手解决局部的排序问题实现对整个大数组的排序，解决一个个小问题，逐步攻克解决整个的问题。

Emphasis

1.从局部到全局的问题解决思路

2.双比对点对数组的遍历以及比较

3.中介数组的数据存放

4.中介数组复制给原数组

5.两个比对点分别到达其极限后需检查另一比对点是否到达极限

6.中介数组复制到原数组时，原数组应该从L坐标开始向后遍历而不是0或1

具体实现

void merge_sort(int q[],int l,int r)
{
    if(l>=r) return;//无法进行的判断
    int mid=l+r>>1;//确定局部解决问题的点
    merge_sort(q,l,mid);//对前半局部进行排序
    merge_sort(q,mid+1,r);//对后半局部进行排序
    
    int k=0;//tmp数组录入和取出的使用坐标
    int i=l;//原数组的第一比对起点
    int j=mid+1;//原数组的第二比对起点
    int tmp[r-l+1];//中介数组，将原数组中排序好的数据进行存储
    while(i<=mid&&j<=r){//下标越界处理
        if(q[i]<=q[j]) tmp[k++]=q[i++];//第一比对点小于第二比对点，则第一比对点向后移动，第二比对点不动，且中介数组tmp中存储第一比对点对应的数
        else tmp[k++]=q[j++];//否则存储第二比对点所对应的数
    }
    while(i<=mid) tmp[k++]=q[i++];//当第二比对点到达其下标极限时，直接把前半部分的数存入中介数组中
    while(j<=r) tmp[k++]=q[j++];//当第一比对点到达其下表极限时，直接把后半部分存入中介数组中
    for(k=0,i=l;i<=r;i++,k++) q[i]=tmp[k];//将tmp数组中已经全部排序好的数重新录入到原数组中，完成排序
}

拓展题目

逆序对的数量:https://www.acwing.com/activity/content/problem/content/822/

二分查找

基本思想

通过两个分别指向头部和尾部的指针，对一个有序数组中的元素进行查找，每一次检查两个指针的中间位置的数，分别作出如下判断

int numbers[];
int left=0
int right=numbers.size()-1;
while(left<=right){
if(numbers[mid]==target) return mid;
if(numbers[mid]<target) left=mid;
if(numbers[mid]>target) right=mid;
}//二分查找的基本思想

Emphasis

1.左右指针

2.中央指针

3.左右指针的越界判断

具体实现

#include<iostream>
using namespace std;
int numbers[100010];//查找数组

int main()
{
    int n;//数组元素个数
    cin>>n;
    int q;//查询次数
    cin>>q;
    for(int i=0;i<n;i++)
    {
        cin>>numbers[i];
    }//输入数据
    while(q-->0){//查询
        int target;//查询数字
        cin>>target;
        int l=0,r=n-1;
        while(l<r)//边界判断
        {
            int mid=l+r>>1;//中间指针
            if(numbers[mid]>=target) r=mid;
            else l=mid+1;
        }//此方法以大于等于目标数为判断条件，所以会得出第一次出现的目标数的坐标
        int left=l;
        if(numbers[l]!=target) cout<<-1<<" "<<-1<<endl;
        else{
            l=0;
            r=n-1;
            while(l<r)
            {
                int mid=l+r+1>>1;
                if(numbers[mid]<=target) l=mid;
                else r=mid-1;
            }//此方法以小于等于坐标数为判断条件，所以会得出最后一次出现的目标数的坐标
            cout<<left<<" "<<l<<endl;
        }//综述，其实就是两次二分查找，通过对于查找方式的改变，得到第一次出现和第二次出现的坐标
    }
    return 0;
}

拓展题目

数的三次方根:https://www.acwing.com/activity/content/problem/content/824/

前缀和

基本思想

前缀和的基本思路在于用一个额外的数组，sums[i]存储原数组第一个数一直到第i个数的和，其中数组遍历不再从0下标开始，为了直观直接从1下标开始，同时也更好理解

//一段数组，假设为{a1,a2,a3,a4,a5}
//则设sums[6]，通过前缀和处理之后sums中的元素为
numebers[6]={0,a1,a2,a3,a4,a5}
sums[6]={0,a1,a1+a2,a1+a2+a3,a1+..+a4,a1+...+a5};

Emphasis

1.前缀和数组的构造

for(int i=1;i<=n;i++)
    {
        sums[i]=sums[i-1]+numbers[i];
    }

2.原数组和前缀和数组的下标都是从1开始，既方便理解，也能更直观的调用

3.当需要得到l-r数字的和时

1	目标段落数据和==sums[r]-sums[l-1]

具体实现

#include<iostream>
using namespace std;

int numbers[100010];
int sums[100010];

int main()
{
    int n;
    cin>>n;
    int m;
    cin>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>numbers[i];
    }
    for(int i=1;i<=n;i++)
    {
        sums[i]=sums[i-1]+numbers[i];
    }
    
    while(m-->0)
    {
        int l,r;
        cin>>l;
        cin>>r;
        cout<<sums[r]-sums[l-1]<<endl;
    }
}

拓展题目

子矩阵的和：https://www.acwing.com/activity/content/problem/content/830/

输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。
#include<iostream>
using namespace std;
const  int N=1010;

int numbers[N][N];//原数组
int sums[N][N];//前缀和数组


int main()
{
    
    int n,m,q;
    cin>>n;
    cin>>m;
    cin>>q;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            cin>>numbers[i][j];
        }
    }
    
    for(int i=1;i<=n;i++)//前缀和数组构造
    {
        for(int j=1;j<=m;j++)
        {
            sums[i][j]=sums[i][j-1]+sums[i-1][j]+numbers[i][j]-sums[i-1][j-1];
        }//其中前缀和构造下标的处理需要注意，总体来说是目标坐标的数+上方所有的和+下方所有的和-重复的左上角所有数的和
    }
    
    while(q-->0)
    {
        int x1,y1,x2,y2;
        cin>>x1;
        cin>>y1;
        cin>>x2;
        cin>>y2;
        cout<<sums[x2][y2]+sums[x1-1][y1-1]-sums[x2][y1-1]-sums[x1-1][y2]<<endl;//此处下标同样需要注意
    }
}

差分

差分作为由前缀和衍生出来的算法思想，具有对某一区间或者某一范围的对象进行集体操作的特性，在对于批量对象进行操作时可以使用

其中，差分数组中的每个元素对应着原数组每个元素相应位置减去前一个数的差，例：
int nums[3]={a1,a2,a3};
int dif[3]={a1-0,a2-a1,a3-a2};
同时差分数组也需要注意下标的起始

差分：https://www.acwing.com/activity/content/problem/content/831/

#include<iostream>
using namespace std;

int numbers[100010];//原数组
int dif[100010];//差分数组
int main()
{
    int n,m,l,r,c;
    cin>>n;//输入数字个数
    cin>>m;//操作数
    for(int i=1;i<=n;i++){
        cin>>numbers[i];
    }
    for(int i=1;i<=n;i++)
    {
        dif[i]=numbers[i]-numbers[i-1];//差分数组构造
    }
    while(m-->0)
    {
        cin>>l;//左起始坐标
        cin>>r;//右结束坐标
        cin>>c;//操作同时加起来的数
        dif[l]+=c;
        dif[r+1]-=c;//下标需要注意
    }
    for(int i=1;i<=n;i++)
    {
        dif[i]+=dif[i-1];//差分数组的重新组合成目标得到的数组
    }
    
    for(int i=1;i<=n;i++)
    {
        cout<<dif[i]<<" ";
    }
}

差分矩阵：https://www.acwing.com/activity/content/problem/content/832/

差分矩阵的构造，实际上就是让原矩阵成为差分矩阵的前缀和数组
dif[x1][y1]+=c;//此操作相当于对以(x1,y1)为左上角直到矩阵最右下角的所有数进行+c操作
dif[x2+1][y1]-=c;//目标区域的右侧需要减去c
dif[x1][y2+1]-=c;//目标区域的下侧需要减去c
dif[x2+1][y2+1]+=c;//(x2,y2)一直到矩阵右下角的所有数加上重复减去的c
for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            dif[i][j]+=mat[i][j];
            dif[i+1][j]-=mat[i][j];
            dif[i][j+1]-=mat[i][j];
            dif[i+1][j+1]+=mat[i][j];
        }
    }//差分矩阵的构造

双指针

基本思想

双指针算法在具体实现过程中，可分为朴素做法以及快捷做法：

其中朴素做法的时间复杂度为O(N^2)，具体实现如下：

for(int i=0;i<n;i++)
{//跑的快的指针
	for(int j=0;j<=i;j++)
    {//跑的慢一点的指针
        if(check(j,i))//check函数为具体判断子串是否有重复的逻辑函数
        {
            res=max(res,j-i+1);//res即可得到最长的不重复连续子串长度
        }
    }
}

Emphasis

双指针有两种具体实现：

1.快慢指针：以一个数组为例，一个指针为慢指针，每次向后遍历一个元素，一个指针为快指针，每次向后遍历两个元素，如此便是快慢指针。

2.对撞指针：同样以数组为例，一个指针设置在数组的头元素，一个指针设置在数组的末尾，两个指针同时向中间移动，直至对撞相遇

在不同的情况下，需要根据实际情况和题目需求确认双指针的具体应用类型：

1.单一序列中的元素操作

2.多个序列中的元素对比

具体实现

例题：给定一个长度为 nn 的整数序列，请找出最长的不包含重复的数的连续区间，输出它的长度。

输入格式

第一行包含整数 nn。

第二行包含 nn 个整数（均在 0∼1050∼105 范围内），表示整数序列。

输出格式

共一行，包含一个整数，表示最长的不包含重复的数的连续区间的长度。

数据范围

1≤n≤10^5

输入样例：

1 2	5 1 2 2 3 5

输出样例：

题解

核心思想

数组边输入就边进行记录数组中元素的次数，输入与记录重复数字同时进行，节省了朴素算法中需要全部输入之后重新遍历的浪费时间的问题

#include<iostream>
using namespace std;

const int N=100010;//数组预留长度
int a[N];//实际数组
int s[N];//用于存储数组中每个元素出现次数的数组

int main()
{
    int n,r=0;
    cin>>n;//数组长度
    
    for(int i=0，j=0;i<n;++i)//指针i很明显是用于数组输入的坐标
    {//指针j则是作为判断，一旦有数字出现了两次，一直将j指针迁移到当前重复的数字坐标上，同时r保留之前片段的最长不重复子段长度
        cin>>a[i];//每一次操作，先输入
        ++ s[a[i]];
        while(s[a[i]]>1) --s[a[j++]];
        r=max(r,i-j+1);//j指针类似于一个同步判定指针，和i指针具有协同作用，并非传统意义上的快慢指针或者对撞指针
    }
    cout<<r;
    
    return 0;
}

A8CF07178F5EF5C953DCBDA82CC53EF4

拓展题目

数组元素的目标和：https://www.acwing.com/problem/content/802/

#include<iostream>
using namespace std;

const int N = 100010;
int A[N];//A数组
int B[N];//B数组

int main()
{
    int n,m,x;
    cin>>n;
    cin>>m;
    cin>>x;
    for(int i=0;i<n;i++)
    {
        cin>>A[i];
    }
    for(int i=0;i<m;i++)
    {
        cin>>B[i];
    }
    
    for(int i=0,j=m-1;i<n;i++)//i指针从A数组从前向后遍历，j指针从B数组从后往前遍历
    {
        while(j>=0&&A[i]+B[j]>x) j--;//普通的条件判断
        if(j>=0&&A[i]+B[j]==x) cout<<i<<" "<<j;
    }
    
    return 0;
}

判断子序列：https://www.acwing.com/problem/content/2818/

#include<iostream>
using namespace std;

const int N=1e5+10;
int a[N],b[N];

int main()
{
    int n,m;
    cin>>n;
    cin>>m;
    for(int i=0;i<n;i++) cin>>a[i];
    for(int j=0;j<m;j++) cin>>b[j];
    
    int i=0;
    for(int j=0;j<m;j++)
    {
        if(i<n&&a[i]==b[j]) i++;
    }
    if(i==n) cout<<"Yes";
    else cout<<"No";
    return 0;
}

位运算

基本思想

首先，位运算中具备以下几大原则

1.按位与 &

两个相应的二进制位都为1，则该位的结果为1，否则为0

2.按位或 |

两个相应的二进制位只要有一个为1，则结果为1

3.按位异或 ^

两个二进制位值相同则为0，否则为1

4.取反 ~

对一个二进制数进行取反，使其位上0变为1，1变为0

5.左移 <<

将一个数的二进制位全部左移N位，右补0

6.右移 >>

将一个数的二进制位右移N位，移到右端的低位被舍弃

Emphasis

具体实现

#include<iostream>
using namespace std;

int main(void)
{
    int n;
    cin>>n;
    
    while (n -- )
    {
        int number;
        int count=0;
        cin>>number;
        while(number>0)
        {
            number=number&(number-1);//核心代码，相当于每一次从当前最低位将一个1在下一次变换中变为0，以此类推，因为如果减一的话，相当于把后面倒数第一个1变为0
            count++;
        }
        cout<<count<<" ";
    }
    return 0;
}

拓展题目

二进制中1的个数:https://www.acwing.com/problem/content/803/

//求二进制数中1的个数
public class Solution {
    public int hammingWeight(int n) {
        int ret = 0;
        for (int i = 0; i < 32; i++) {
            if ((n & (1 << i)) != 0) {//左移一位等价于乘以2
                ret++;
            }
        }
        return ret;
    }
}

//技巧:n&(n-1)操作可以消除二进制数中的最后一个1

拓展题目2:

//给你一个整数 n，请你判断该整数是否是 2 的幂次方。如果是，返回 true ；否则，返回 false 。
//如果存在一个整数 x 使得 n == 2x ，则认为 n 是 2 的幂次方。

class Solution {
    public boolean isPowerOfTwo(int n) {
        return n > 0 && (n & (n - 1)) == 0;
    }
}

离散化

基本思想

离散化，把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。

通俗的说，离散化是在不改变数据相对大小的条件下，对数据进行相应的缩小。例如：

原数据：1,999,100000,15；处理后：1,3,4,2；

原数据：{100,200}，{20,50000}，{1,400}；

处理后：{3,4}，{2,6}，{1,5}；

Emphasis

离散化的基本思路是，先排序，再删除重复元素，最后就是索引元素离散化后对应的值

区间和题解.png

在离散化做法中，没有必要按照规定的顺序，将对应的操作插入到相应的位置中，只需要利用好其相对位置的关系，就可以节省大量的空间以及时间，

“相对位置”这个概念非常重要

具体实现

例题：

假定有一个无限长的数轴，数轴上每个坐标上的数都是 0。

现在，我们首先进行 nn次操作，每次操作将某一位置 x 上的数加 c。

接下来，进行 m 次询问，每个询问包含两个整数 l 和 r，你需要求出在区间 [l,r][l,r] 之间的所有数的和。

输入格式

第一行包含两个整数 n 和 m。

接下来 n 行，每行包含两个整数 x 和 c。

再接下来 m 行，每行包含两个整数 l 和 r。

输出格式

共 m 行，每行输出一个询问中所求的区间内数字和。

输入样例：

输出样例：

8
0
5
#include<iostream>
#include <vector>
#include<algorithm>
//基本头文件
using namespace std;

typedef pair<int, int> PII;//定义PII数对

const int N = 300010;

int n,m;//n为操作次数，m为查询次数
int a[N],s[N];//数组a[N]是原数串,s[N]是前缀和处理数组

vector<int> alls;//alls存储与操作相关的所有坐标
vector<PII> add,query;

int find(int x) 
{//find函数用于在alls容器中找到对应的坐标
    int l=0,r=alls.size()-1;
    while(l<r)
    {
        int mid=l+r>>1;
        if(alls[mid]>=x) r=mid;
        else l=mid+1;
    }
    return r+1;
}

int main()
{
    cin>>n>>m;
    for(int i=0;i<n;i++)
    {//此处add容器作用是存储相应坐标上加减的数，alls容器的作用是存储有过操作的坐标
        int x,c;
        cin>>x>>c;
        add.push_back({x,c});
        
        alls.push_back(x);
    }
    
    for(int i=0;i<m;i++)
    {//query容器的作用很明显是作为存放查询左端和右端坐标的数对容器
        int l,r;
        cin>>l>>r;
        query.push_back({l,r});
        
        alls.push_back(l);
        alls.push_back(r);
    }
    
    //去重
    sort(alls.begin(),alls.end());//对alls进行排序
    alls.erase(unique(alls.begin(),alls.end()),alls.end());//对alls中的元素进行去重
    
    //处理插入
    for(auto item:add)
    {
        int x=find(item.first);
        a[x]+=item.second;
    }//将add数对容器中的数对提取出来，进行对数串上的操作
    
    //预处理前缀和
    for(int i=1;i<=alls.size();i++) s[i]=s[i-1]+a[i];
    
    //处理询问
    for(auto item:query)//query中每个元素都是数对
    {
        int l=find(item.first),r=find(item.second);
        cout<<s[r]-s[l-1]<<endl;
    }
    
    return 0;
}
在上述代码中，一共用到了三个容器，分别是
1.整型数据容器alls
	作用：存储与操作相关的所有坐标
2.整型数对容器add
	作用：存储对数串上每个坐标的操作详细，存储每个点坐标和对点坐标上加减的数对
3.整型数对容器query
	作用：存储每一次查询的数串区间

区间合并

基本思想

1.按区间左端点进行排序

2.通过比对右端点产生的不同情况进行不同的操作

三种情况：

绿色情况：用原区间覆盖，即不变

橙色情况：延长ed的长度

粉色情况：无交集，当前比较区间就可以独立出来了

Emphasis

注意题目给出的端点判断依据即可

具体实现

#include<iostream>
#include<algorithm>
#include <vector>

using namespace std;

const int N = 100010;

typedef pair<int, int> PII;//数对，用于存放输入的每一个区间

vector<PII> segs;//区间的存储容器

void merge(vector<PII> &segs)//区间的合并函数
{
    vector<PII> res;//返回的答案区间
    
    sort(segs.begin(),segs.end());//先对原区间以每个数对的第一个数为基准进行排序
    
    int st=-2e9,ed=-2e9;//设置边界
    for(auto seg:segs)//对每一个小区间进行单独判断以及操作
    {
        if(ed<seg.first)
        {//具体的逻辑实现
            if(st!=-2e9) res.push_back({st,ed});
            st=seg.first,ed=seg.second;
        }
        else ed=max(ed,seg.second);
    }
    
    if(st!=-2e9) res.push_back({st,ed});
    
    segs=res;
}
int main()
{
    int n;
    cin>>n;
    while (n -- )
    {
        int l,r;
        cin>>l;
        cin>>r;
        segs.push_back({l,r});
    }
    
    merge(segs);
    
    cout<<segs.size()<<endl;
    
    return 0;
    
}

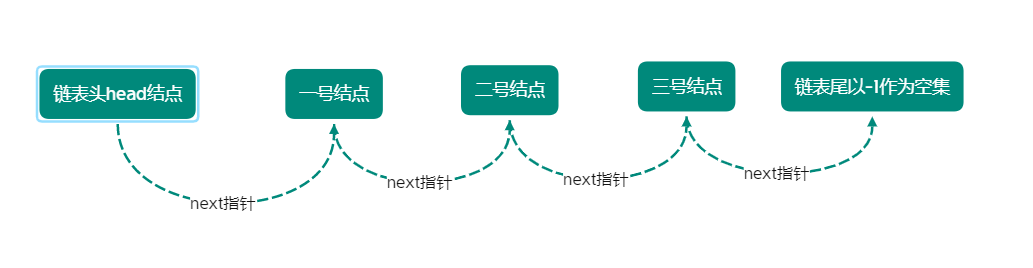
数据结构

单链表

结构特征

单链表是由一个个链表节点构成的一个整体，其中每个结点具有其权值和指向后一结点的指针，此处以数组的形式模拟链表

struct Node
{
    int val;//权值
    Node *next;//指向下一结点的指针
}//单一结点的定义

new node();//非常慢

//在实际工程和算法题目中，一般不采用动态列表以及以new方法创建结点的方式构造链表，其速度太慢，适用面很窄

普通的插入函数

#include <iostream>
using namespace std;
//Declare Node
struct Node{
    int num;
    Node *next;
};
//Declare starting (Head) node
struct Node *head=NULL;
//Insert node at start
void insertNode(int n){
    struct Node *newNode=new Node;
    newNode->num=n;
    newNode->next=head;
    head=newNode;
}

代码实现

数组版本

#include<iostream>
using namespace std;
const int N=100010;
//head表示头结点的下标
//e[i]表示节点i的值
//ne[i]表示结点i的next指针是多少
//idx存储当前已经用到了哪个点
int idx,head,e[N],ne[N];
int a;
void add_head(int x){//头结点插入
    e[idx]=x;//先将最新结点赋值
    ne[idx]=head;//将idx结点的指针进行对应的操作
    head=idx++;//idx向后移动一位，head也向后移动一位
}
void add(int k,int x){//k结点之后插入
    e[idx]=x;//先对最新点赋值
    ne[idx]=ne[k];//改变新结点指针的指向
    ne[k]=idx++;//前一个结点的next指针重新指向新结点
}
void remove(int k){//删除第k个结点
    ne[k]=ne[ne[k]];
}

int main(){
    head=-1;idx=0;
    cin>>a;
    while(a--){
        string op;
        int k,x;
        cin>>op;
        if(op=="D")//删除第k个数后面的数
        {

            cin>>k;
            if(!k)head=ne[head];
            remove(k-1);
        }
        else if(op=="H")//表头插入
        {
            cin>>x;
            add_head(x);
        }
        else if(op=="I"){//指定位置插入
            int k,x;
            cin>>k>>x;
            add(k-1,x);
        }
    }
    for(int i=head;i!=-1;i=ne[i])
      cout<<e[i]<<" ";
    return 0;

}
//此处采用的是用数组模拟单链表的方式

CCF282EEFE571D40F6829209498ECD7B

指针版本

class MyLinkedList {

private://私人函数定义
    int size;//表示链表长度
    node *head;//定义头指针

public:
    struct node{//单链表节点结构
        int val;//数据域
        node *next;//指针域
        node(int x): val(x),next(NULL){}//表示的含义就是节点数值为x，指针为空（初始化一个新节点）
    };

    MyLinkedList() {//初始化链表
        head=new node(0);
        size=0;
    }
    
    int get(int index) {//获取索引节点数值
        if(index<0||index>(size-1)) return -1;//索引比0小或者比最大索引大，返回-1
        node *cur=head->next;//辅助指针指向第一个节点
        while(index--) cur=cur->next;//循环index次遍历到第index个节点
        return cur->val;//指向数值输出
    }
    
    void addAtHead(int val) {//插入头
        node *newnode=new node(val);//创建新节点
        newnode->next=head->next;//将头节点的next赋值给新的节点--->相当于连接新插入节点与第一个节点
        head->next=newnode;//连接头指针与第一个新节点
        size++;//长度加1
    }
    
    void addAtTail(int val) {//插入尾
        node *cur=head;//辅助指针从头指针开始
        while(cur->next) cur=cur->next;//遍历到最后一个节点,如果是空链表，则直接不循环，指针还是在头指针
        node *newnode=new node(val);//创造新节点并赋值
        newnode->next=cur->next;//复制原最后节点的next信息
        cur->next=newnode;//连接最后一个新节点和上一个节点
        size++;//长度加1
    }
    
    void addAtIndex(int index, int val) {
        if(index<=0) addAtHead(val);//插入index的时候，如果下标是=0,就相当于从头插入，所以要包含<=
        else if(index==size) addAtTail(val);
        else if(index>size) return ;
        else{
            node *newnode=new node(val);
            node *cur=head;//辅助指针从头指针开始
            while(index--) cur=cur->next;
            newnode->next=cur->next;//连接index
            cur->next=newnode;//连接前一个
            size++;//长度+1
        }
    }
    
    void deleteAtIndex(int index) {
        if(index<0||index>=size) return ;
        node *cur=head;//从头指针开始
        while(index--){//遍历到index-1的位置,循环次数是index次
            cur=cur->next;
        }
        cur->next = cur->next->next;//相当于直接跨过了index节点
        size--;
    }
};

双链表

结构特征

双链表不同于单链表，其中每一个结点除了指向下一结点的指针以外，还具有指向前一结点的指针

struct Node{
    int val;//权值
    Node *pre;
    Node *next;
}

代码示例

数组版本

#include<iostream>
#include<algorithm>
#include<string.h>

using namespace std;

const int N = 100010;

int e[N],l[N],r[N],idx;//l[N]存储左结点指针，r[N]存储右结点指针

void init()//初始化
{
    r[0]=1,l[1]=0;//最初的两个点进行初始化处理
    idx=2;
}

void add(int k,int x)//在第k个结点的右边插入权值为x的结点
{
    e[idx]=x;//权值赋值
    r[idx]=r[k];
    l[idx]=k;
    l[r[k]]=idx;
    r[k]=idx++;
}

void remove(int k)//删除第k个结点
{
    r[l[k]]=r[k];
    l[r[k]]=l[k];
}


int main()
{
    int m;
    cin>>m;
    init();
    while (m -- )
    {
        string op;
        int k,x;
        cin>>op;
        
        if(op=="L")
        {
            cin>>x;
            add(0,x);
        }
        else if(op=="R")
        {
            cin>>x;
            add(l[1],x);
        }
        else if(op=="D")
        {
            cin>>k;
            remove(k+1);
        }
        else if(op=="IL")
        {
            cin>>k>>x;
            add(l[k+1],x);
        }
        else
        {
            cin>>k>>x;
            add(k+1,x);
        }
    }
    
    for(int i=r[0];i!=1;i=r[i]) cout<<e[i]<<" ";
    cout<<endl;
    
    return 0;
}

指针版本

class MyLinkedList {
struct ListNode
{//结点定义
    int val;//权值
    ListNode* prev;//前驱指针
    ListNode* next;//后驱指针
    ListNode(int x):val(x),prev(this),next(this){}
};
public:
    
    MyLinkedList() {//创建函数
        head = new ListNode(-1);
        size = 0;
    }
    

    int get(int index) {//查找函数
        ListNode* pos =head;//先安排一个结点从头开始
        while(index-->=0){//向后遍历
            pos=pos->next;
            if(pos==head) //如果就一个结点，直接返回权值
                return head->val;
        } 
        return pos->val;
    }
    
   
    void addAtHead(int val) {//头插
        ListNode* node =new ListNode(val);//先建立一个新结点并赋值
        node->next = head->next;
        head->next = node;
        node->next->prev=node;
        node->prev=head;
        size++;
    }
    
    
    void addAtTail(int val) {//尾插
        ListNode* node =new ListNode(val);
        node->prev = head->prev;
        head->prev = node;
        node->prev->next = node;
        node->next = head;
        size++;
    }
    
    
    void addAtIndex(int index, int val) {
        ListNode* pos = head;
        if(index==size)
        {
            addAtTail(val);
        }else
        {
            //定位到插入位置
        while(index-->=0){
            pos=pos->next;
            if(pos==head) 
            {
                return ;
            }                
        }
        ListNode* node = new ListNode(val);
        node->prev = pos->prev;
        pos->prev = node;
        node->prev->next = node;
        node->next = pos;
        size++;
        }                
    }
    
 
    void deleteAtIndex(int index) {//删除结点
        ListNode* pos = head;
        while(index-->=0){
            pos=pos->next;
            if(pos==head) 
                return ;            
        }
        ListNode* temp = pos->next;
        pos->next->prev =pos->prev;
        pos->prev->next = temp;
        size--;

    }
private:
    int size;
    ListNode* head;
};

栈

结构特征

在数据结构栈中，可以用FILO即first in last out即先进后出概括其特点，最先进入栈中的元素在执行出栈操作时，反而最后出栈，就好像抽纸，最先放入的那张纸反而最后才会抽出来

代码实现

#include<iostream>
using namespace std;

const int N=100010;

int stack[N];
int idx=-1;

void push(int x)//压栈
{
    stack[++idx]=x;
}

void empty()//空栈判断
{
    if(idx>=0) cout<<"NO"<<endl;
    else
    {
        cout<<"YES"<<endl;
    }
}

void pop()
{
    idx--;
}

void query()
{
    cout<<stack[idx]<<endl;
}


int main()
{
    int M;
    string op;
    while (M -- )
    {
        cin>>op;
        if(op=="push")
        {
            int x;
            cin>>x;
            push(x);
        }
        else if(op=="pop")
        {
            pop();
        }
        else if(op=="empty")
        {
            empty();
        }
        else if(op=="query")
        {
            query();
        }
    }
}

扩展题目

表达式求值：https://www.acwing.com/problem/content/3305/

#include<iostream>
#include<string>
#include<stack>
#include<unordered_map>
using namespace std;

stack<int> nums;//数值栈
stack<char> op;//操作符栈

unordered_map<int,char> h{{'+', 1}, {'-', 1}, {'*',2}, {'/', 2}};//优先级对应表

void eval()
{
    int a=nums.top();
    nums.pop();
    int b=nums.top();
    nums.pop();//取出数值栈中的两个数
    
    char opr=op.top();
    op.pop();
    
    int r=0;
    if(opr=='+') r=a+b;
    if(opr=='-') r=a-b;
    if(opr=='*') r=a*b;
    if(opr=='/') r=a/b;
    
    nums.push(r);
}


int main()
{
    string exp;
    cin>>exp;
    
    for(int i=0;i<exp.size();i++){
        if(isdigit(exp[i])){
            int x=0,j=i;
            while(j<exp.size()&&isdigit(exp[j]))
            {
                x=x*10+exp[j]-'0';
                j++;//因为计算中不可能只有一位数，比如12，但是遍历的时候是一个一个字符遍历的，所以对于连续的多位数字，我们需要采取能够保留完整计算数的方法
            }
            nums.push(x);
            i=j-1;
        }
        else if(exp[i]=='(')
        {
            op.push(exp[i]);
        }
        else if(exp[i]==')')
        {
            while(op.top()!='(')
                eval();
            op.pop();
        }
        else{
            while(op.size()&&h[op.top()]>=h[exp[i]])
                eval();
            op.push(exp[i]);
        }
    }
    while(op.size()) eval();
    cout<<nums.top()<<endl;
    
    return 0;
}

单调栈：https://www.acwing.com/problem/content/832/

#include<iostream>
using namespace std;

const int N=100010;
int stck[N];//操作栈
int top=0;//栈顶坐标

int main()
{
    int n;
    cin>>n;
    while(n--){
        int x;
        cin>>x;
        while(top&&stck[top]>=x) top--;//栈不为空且栈顶元素大于即将入栈元素时，
        if(!top) cout<<"-1 ";//一旦栈空，则说明左侧没有小于x的数
        else{
            cout<<stck[top]<<" ";
        }
        stck[++top]=x;
    }
    
    return 0;
}

滑动窗口

结构特征

单调队列顾名思义，是具有单调性的队列，具体表现为通过入队元素与队尾元素比较再进行操作

代码实现

#include<iostream>
using namespace std;

const int N=1000010;

int numbers[N];//原数组
int queue[N];//单调队列，此队列中存储的并不是具体的数，而是元素的下标

//对于queue单调队列，其本身有以下特性：
//1.内部存储的并不是原数组中具体的数，而是其下标
//2.其队首的元素为当前最小的元素，即队首的数总是最小的
//形象的理解滑动窗口，当前三位完成比较时，直接向后滑一位，因为前两位已经比对出更小的那一位了
//且其坐标已经存入了queue队列首位，所以只需要看新加入的一位数的相对大小即可

int main()
{
    int n,k;
    cin>>n>>k;
    for(int i=0;i<n;i++) cin>>numbers[i];

    int head=0,tail=-1;
    for(int i=0;i<n;i++)
    {
        if(head<=tail&&i-k+1>queue[head]) head++;//队列不为空，且最小的一位已经不在滑动窗口内，向后滑动一位
        while(head<=tail&&numbers[queue[tail]]>=numbers[i]) tail--;//入队数大于队尾数，队尾数出列

        queue[++tail]=i;//直接存储下下标即可
        if(i-k+1>=0)cout<<numbers[queue[head]]<<" ";
    }

    cout<<"\n";

    head=0,tail=-1;
    for(int i=0;i<n;i++)
    {//大致思路同上，但是具体条件改变
        if(head<=tail&&i-k+1>queue[head]) head++;
        while(head<=tail&&numbers[queue[tail]]<=numbers[i]) tail--;

        queue[++tail]=i;
        if(i-k+1>=0) cout<<numbers[queue[head]]<<" ";
    }

    return 0;
}

拓展题目:字符串的排列:https://leetcode-cn.com/problems/permutation-in-string/

class Solution {
    public boolean checkInclusion(String s1, String s2) {
        int m = s1.length(), n = s2.length();
        if (m > n) return false;

        int[] cnt = new int[26];
        for (char c : s1.toCharArray()) cnt[c - 'a']++;
        
        int[] cur = new int[26];
        for (int i = 0; i < m; i++) cur[s2.charAt(i) - 'a']++;
        
        if (check(cnt, cur)) return true;
        
        for (int i = m; i < n; i++) {
            cur[s2.charAt(i) - 'a']++;
            cur[s2.charAt(i - m) - 'a']--;
            if (check(cnt, cur)) return true;
        }//滑动窗口
        return false;
    }
    
    boolean check(int[] cnt1, int[] cnt2) {
        for (int i = 0; i < 26; i++) {
            if (cnt1[i] != cnt2[i]) return false;
        }
        return true;
    }
}

KMP

算法特征

KMP算法作为一种字符串匹配算法，可在一个字符串S中找出一个词W出现的位置。一个词在不匹配时本身就包含足够的信息来确定下一个匹配可能开始的位置，这种算法可以避免重新检查先前已经匹配过的字符，更加节约时间

暴力写法

#include<iostream>
using namespace std;

const int N = 100010;

char p[N];
char s[N];

int main()
{
    int N;
    cin>>N;
    for(int i=0;i<N;i++)
    {
        cin>>p[i];
    }
    
    int M;
    cin>>M;
    for(int i=0;i<M;i++)
    {
        cin>>s[i];
    }
    
    for(int i=0;i<M;i++)
    {
        bool flag=true;
        for(int j=0;j<N;j++)
        {
            if(p[j]!=s[i+j]){
                flag=false;
                break;
            }
        }
        if(flag) cout<<i<<" ";
    }
}

然而暴力写法的话，就失去了节约时间的意义，所以我们采用耗时更少的KMP

代码实现

在用具体代码实现之前，需要清楚一个重点，就是在两个字符串匹配的时候，分别指向它们的指针都是同步运行，没有改变位置的时候，都是一趟从头到尾，没有多余的操作，而原字符串也是不动的，所有元素中，唯一活动的只有匹配子字符串，它随着自己的遍历指针结合next数组对应的元素而动，三动一不动！

//在kmp算法中，主要由两大重点构成，分别是1.next数组 2.匹配
//1.next数组
//其实next数组非常好得出，举例，比如字符串abcab，我们假设此时对于字符串的遍历指针i已经指到了最后一位，即i=5
//其前缀集合{a,ab,abc,abca}
//其后缀集合{b,ab,cab,bcab}
//通过观察前缀集合以及后缀集合，发现其公共最长前后缀集合串为ab，长度为2，所以next[i]也就是next[5]=2
//示例：字符串p

for(int i=2,j=0;i<=p.size();i++)
{
    while(j&&p[j+1]!=p[i]) j=next[j];//这里其实很好理解，就是字符串p自己和自己匹配，从而得出next数组中的内容
    //当失配时，就可以将此点坐标记录在next中了
    if(p[j+1]==p[i]) j++;
    next[i]=j;//记录下前面与自己匹配的最末坐标
}


//2.匹配
//匹配的思路很简单，与next数组的构造过程相差无几，只是有一些细节需要注意

for(int i = 1, j = 0; i <= n; i++)
{
    while(j && s[i] != p[j+1]) j = ne[j];
    //如果j有对应p串的元素， 且s[i] != p[j+1], 则失配， 移动p串
    //用while是由于移动后可能仍然失配，所以要继续移动直到匹配或整个p串移到后面（j = 0)

    if(s[i] == p[j+1]) j++;
    //当前元素匹配，j移向p串下一位
    if(j == m)
    {
        //匹配成功，进行相关操作
        j = next[j];  //继续匹配下一个子串
    }
}

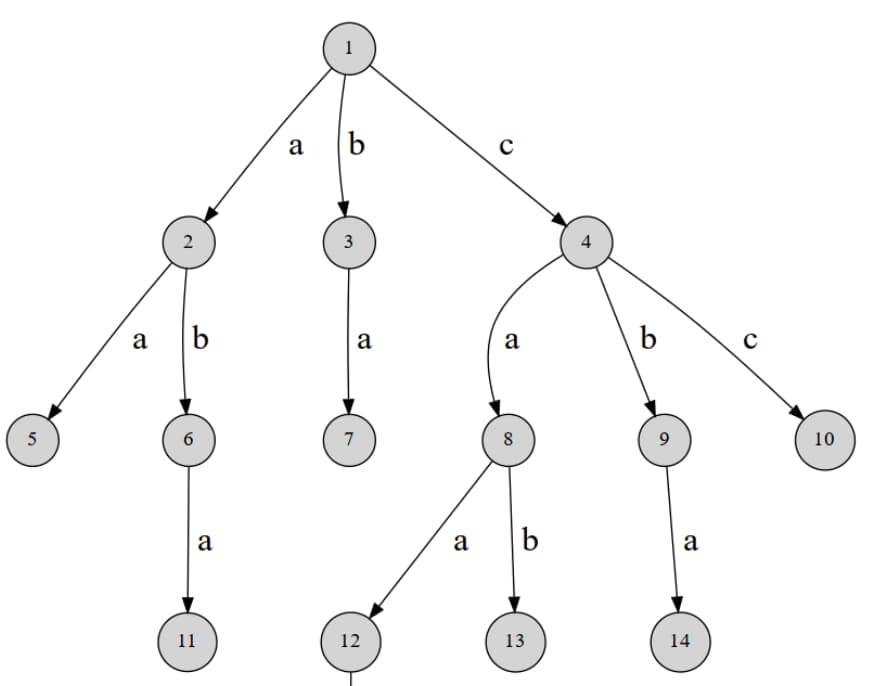
Trie(字典树)

结构特征

Trie树是经常用来存储字符串集合的一种数据结构，即称为字典树，它的具体结构如下

从根结点延伸出许多的分支，其中每一条边代表着一个后继字母

将代码和具体结构图像抽象之后，就可以得出下面这张图

BA64E728F2026ECA6758D23B9D1225F7

代码实现

1.首先我们要清楚idx是干什么的
如讲解所说，idx在插入时，就是进行边的开拓，我的理解中，字母代表的是字典树中的边(如有错误请见谅),idx则在不存在此条分支时开拓新的结点为其提供叶子结点且是配合cnt数组进行计数的关键
2.我的理解中，p=son[p][u]这一步非常的巧妙，进行抽象之后，发现就是这一步让字典树的查询能进入相应的下一级
3.字典树最大的特点，就是存储公共前缀，避免不必要的开支

#include<iostream>
#include<string>

using namespace std;

const int N = 100010;

int son[N][26],cnt[N],idx;
char str[N];

void insert(char *str)  // 插入
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
    cnt[p] ++ ;
}

int query(char *str)  // 查询
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

int main()
{
    int n;
    cin>>n;
    while (n -- ){
        char op[2];
        cin>>op;
        cin>>str;
        if(*op=='I') insert(str);
        else{
            cout<<query(str)<<endl;
        }
    }

    return 0;
}

扩展题目

最大异或对:https://www.acwing.com/problem/content/description/145/

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 100010, M = N * 31;

int n;
int a[N];
int son[M][2], idx;//异或对的话，其trie的结构就是分支只有0和1两种可能性

void insert(int x)
{
    int p = 0;
    for (int i = 30; i >= 0; i--) {
        int u = x >> i & 1;//这句话的意义相当于得到x上第i位的数字
        if (!son[p][u]) son[p][u] = ++idx;
        p = son[p][u];
    }
}

int query(int x) {
    int p = 0, res = 0;
    for (int i = 30; i >= 0; i--) {
        int u = x >> i & 1;
        if (son[p][!u]) {
            p = son[p][!u];
            res = res * 2 + !u;
        }
        else {
            p = son[p][u];
            res = res * 2 + u;
        }
    }

    return res;
}


int main()
{
    scanf("%d", &n);
    int res = 0;
    for (int i = 0; i < n; i++) scanf("%d", &a[i]);

    for (int i = 0; i < n; i++)
    {
        insert(a[i]);
        int t = query(a[i]);
        res = max(res, a[i] ^ t);
    }

    printf("%d", res);

    return 0;
}

并查集

算法思想

并查集用来快速处理这样的问题：

将两个集合合并
询问两个元素是否在同一个集合当中

基本原理

每个集合用一棵树来表示。树根的编号就是整个集合的编号。每个节点存储它的父节点，p[x]表示x的父节点

问题1：如何判断树根：if(p[x]==x)

问题2：如何求x的集合编号：while(p[x]!=x) x=p[x];

问题3：如何合并两个集合：px是x的集合编号，py是y的集合编号。p[x]=y

例题描述

一共有 nn 个数，编号是 1∼n1∼n，最开始每个数各自在一个集合中。

现在要进行 mm 个操作，操作共有两种：

M a b，将编号为 aa 和 bb 的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；
Q a b，询问编号为 aa 和 bb 的两个数是否在同一个集合中；

输入格式

第一行输入整数 nn 和 mm。

接下来 mm 行，每行包含一个操作指令，指令为 M a b 或 Q a b 中的一种。

输出格式

对于每个询问指令 Q a b，都要输出一个结果，如果 aa 和 bb 在同一集合内，则输出 Yes，否则输出 No。

每个结果占一行。

数据范围

1≤n,m≤10^5

输入样例：

输出样例：

1
2
3

Yes
No
Yes

代码实现

#include<iostream>
using namespace std;

const int N = 100010;

int n,m;
int p[N];

int find(int x){//返回x的集合祖宗节点+路径压缩
    if(p[x]!=x) p[x]=find(p[x]);//如果
    return p[x];
    
}
int main()
{
    scanf("%d%d", &n, &m);
    
    for(int i=0;i<=n;i++) p[i]=i;
    
    while (m -- ){
        char op[2];
        int a,b;
        scanf("%s%d%d",op,&a,&b);
        
        if(op[0] =='M') p[find(a)]=find(b);
        else
        {
            if(find(a)==find(b)) puts("Yes");
            else{
                puts("No");
            }
        }
    }
    
    return 0;
    
}

拓展题目

连通块中点的数量:https://www.acwing.com/problem/content/839/

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100010;
int n,m;
int p[N],cnt[N];//p数组是父节点数组，cnt数组是每个父节点中节点个数的计数数组

int find(int x){//祖宗节点寻找函数
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        p[i]=i;
        cnt[i]=1;
    }
    
    while (m -- ){
        string op;
        int a,b;
        cin>>op;
        if(op=="C"){
            cin>>a>>b;
            a=find(a);
            b=find(b);
            if(a!=b){//如果两个点相同，就没有连接的必要
                p[a]=b;
                cnt[b]+=cnt[a];
            }
        }else if(op=="Q1"){
            
            cin>>a>>b;
            if(find(a)==find(b)){
                cout<<"Yes"<<endl;
            }else{
                cout<<"No"<<endl;
            }
        }else{
            cin>>a;
            cout<<cnt[find(a)]<<endl;
        }
    }
    return 0;
}

食物链:https://www.acwing.com/problem/content/242/

#include<iostream>
using namespace std;

const int N = 50010;

int n,k;
int p[N],d[N];//p[N]是所有物种的根节点，d[N]是物种到根节点的距离

//这道题可以根据节点距离根节点的长度来确定节点种类
//1.与根节点距离模3余0，则就是根节点同物种
//2.与根节点距离模3余1，则吃根节点代表物种
//3.与根节点距离模3余2，则被根节点吃

int find(int x){//寻找根节点函数
    if(p[x]!=x){
        int t=find(p[x]);//先保存根节点
        d[x]+=d[p[x]];//节点x需要加上其根节点到最终根节点的距离
        p[x]=t;
    }
    return p[x];
}

int main()
{
    scanf("%d%d",&n,&k);
    
    for(int i=1;i<=n;i++) p[i]=i;//定义各自的根节点
    
    int res=0;
    
    while(k--){
        int t,x,y;
        scanf("%d%d%d",&t,&x,&y);
        
        if(x>n||y>n) res++;
        else{
            int px=find(x),py=find(y);
            if(t==1){//x和y是同类
                if(px==py&&(d[y]-d[x])%3) res++;//如果x和y是同一种族圈且满足被吃或吃的关系，则为假话
                else if(px!=py){
                    p[px]=py;//将px的根节点接到y的根节点上
                    d[px]=d[y]-d[x];//d[x]作出相应的更改
                }
            }else{//吃或被吃情况
                if(px==py&&(d[y]-d[x]+1)%3) res++;
                else if(px!=py){
                    p[px]=py;
                    d[px]=d[y]+1-d[x];
                }
            }
        }
    }
    cout<<res;
    
    return 0;
}

堆

结构特征

堆的用途:

插入一个数

1	heap[++size]=x;up(size);

求集合当中的最小值

heap[1]

删除最小值

1	heap[1]=heap[size];size--;down(1);

删除任意一个元素

heap[k]=heap[size];
size--;
down(k);
up(k);

修改任意一个元素

1
2
3

heap[k]=x;
down(k);
up(k);

堆的结构可以抽象为一颗完全二叉树，除开最后一层结点以外上面的层数都是满树

代码实现

堆排序:https://www.acwing.com/problem/content/840/

import java.util.Scanner;

public class HeapTest {
    static int N=1000010;
    static int n;
    static int m;
    static int cnt;
    static int[] h=new int[N];

    public static void down(int u){//下沉
        int t=u;
        if(u*2<=cnt&&h[u*2]<h[t]) t=u*2;
        if(u*2+1<=cnt&&h[u*2+1]<h[t]) t=u*2+1;
        //这里是三者比较，分别是根节点，右子节点和左子节点一起比较
        if(u!=t){
            int s=h[u];
            h[u]=h[t];
            h[t]=s;
            down(t);
        }
    }

    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        n=sc.nextInt();
        m=sc.nextInt();
        for(int i=1;i<=n;i++){
            h[i]=sc.nextInt();
        }
        cnt=n;

        for(int i=n/2;i!=0;i--) down(i);

        while(m!=0){
            System.out.print(h[1]+" ");
            h[1]=h[cnt--];
            down(1);
            m--;
        }

        System.out.println();
    }
}

拓展题目

模拟堆:https://www.acwing.com/problem/content/841/

哈希表

结构特征

散列表也叫哈希表，是一种根据关键码值(key value)直接进行访问的数据结构，一般情况下是通过模运算得到码值，然后放入对应的散列中

代码实现

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int N=100003;//这里的模运算数最好是选用大于数据量的第一个质数
    static int[] h=new int[N];//h数组为散列数组，其中存放各个码值对应的拉链
    static int[] e=new int[N];//e数组和下面的ne数组相当于构成链表，也就是拉链
    static int[] ne=new int[N];
    static int idx=0;//记录点的个数

    static void Insert(int x){//插入函数
        int k=(x%N+N)%N;//取模运算
        e[idx]=x;
        ne[idx]=h[k];
        h[k]=idx++;
    }

    static boolean find(int x){
        int k=(x%N+N)%N;
        for(int i=h[k];i!=-1;i=ne[i]){
            if(e[i]==x){
                return true;
            }
        }
        return false;
    }

    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        Arrays.fill(h,-1);
        int n;
        n= sc.nextInt();
        while(n-->0){
            String op=sc.next();

            int x=sc.nextInt();
            if(op.equals("I")){
                Insert(x);
            }else{
                if(find(x)) System.out.println("Yes");
                else{
                    System.out.println("No");
                }
            }
        }

    }
}

如果对于其中的逻辑不太清楚，下面是debug中数据的具体表现

样例数据:

7
I 1
I 2
I 3
I 3
I 2
I 1
Q 1

调试结果:

拓展题目

字符串哈希:https://www.acwing.com/problem/content/843/

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int N=100010,P=131;
    static long[] h=new long[N];
    static long[] p=new long[N];//存放p的n次幂
    public static long get(int l,int r){
        return h[r]-h[l-1]*p[r-l+1];//相当于把两个区间中的字符串对齐求出哈希值
    }

    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt();
        int m=sc.nextInt();

        String s= sc.next();
        p[0]=1;
        for(int i=1;i<=n;i++){
            p[i]=p[i-1]*P;//预处理
            h[i]=h[i-1]*P+s.charAt(i-1);//求下一位的哈希值直接*p加上下一个字符的ascii码值即可
        }

        while(m-->0){
            int l1= sc.nextInt();
            int r1= sc.nextInt();
            int l2= sc.nextInt();
            int r2= sc.nextInt();
            if(get(l1,r1)==get(l2,r2)) System.out.println("Yes");
            else
                System.out.println("No");
        }
    }
}

搜索与图论

DFS(深度优先搜索)

基本思想

深度优先搜索顾名思义，即探索访问一棵树中的叶结点,就好比一颗树中有各条不同的路径，我们的目标就是分别把每一条路走到尽头，达到每一条路的终点即可。

Emphasis

dfs深度优先搜索的精髓在于其递归回溯过程中对于条件的书写以及还原回溯前状态的操作,利用好先前所进行的操作改变各结点的访问状态，在递归过程中加以利用

具体实现

例题:

给定一个整数 nn，将数字 1∼n1∼n 排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入格式

共一行，包含一个整数 nn。

输出格式

按字典序输出所有排列方案，每个方案占一行。

数据范围

1≤n≤7

输入样例：

输出样例：

代码实现

#include<iostream>
using namespace std;

const int N=10;
int path[N];//path数组顾名思义，就是走一条路径，把路径上的所有数记录下来，然后存着，便于最后打印
bool st[N];
int n;

void dfs(int u)//u是起始的状态
{
    if(u==n)//n是元素的个数
    {//当u==n即状态中的元素达到最大个数时，就可以直接打印了
        for(int i=0;i<n;i++) cout<<path[i]<<" ";
        puts("");
        return;
    }
    
    for(int i=1;i<=n;i++)
    {//从1开始
        if(!st[i]){//如果数字i还没有被放入状态中，就把它存到path里面去
            path[u]=i;
            st[i]=true;//因为数字i在前面的path里面已经被使用过了，所以变更st[i]的状态
            dfs(u+1);//基于前一个数已经纳入path的前提下，对下一层进行dfs
            st[i]=false;//在对一个从头到尾的完整状态进行dfs之后，要对用完的元素进行还原，相当于返回上一层，重新归纳
        }
    }
}

int main()
{
    cin>>n;
    dfs(0);
    return 0;
}

拓展题目

n-皇后问题:https://www.acwing.com/problem/content/845/

#include<iostream>
using namespace std;

const int N=20;
int n;
char chess[N][N];
bool col[N],dg[N],udg[N];//col是行与列上是否有皇后的判断数组，dg为正对角线，udg为反对角线上是否有皇后的判断数组

void dfs(int u)
{
    if(u==n){//同样，一旦皇后棋子全部填入了棋盘，我们就可以将此种方案的棋盘进行打印
        for(int i=0;i<n;i++) puts(chess[i]);
        puts("");
        return;
    } 
    for(int i=0;i<n;i++)
    {
        if(!col[i]&&!dg[u+i]&&!udg[n-u+i]){//此处i的含义，是第i个皇后即将要填入棋盘
            chess[u][i]='Q';//可以直接把chess[u][i]设为Q的原因是，除开小棋盘的情况，其他情况一行最起码都是有一个皇后棋子的
            col[i]=dg[u+i]=udg[n-u+i]=true;
            dfs(u+1);
            /*以下两行是为了还原dfs之前的状态*/
            col[i]=dg[u+i]=udg[n-u+i]=false;
            chess[u][i]='.';
        }
    }
}
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            chess[i][j]='.';
        }
    }
    
    dfs(0);
    
    return 0;
}

BFS(广度优先搜索)

基本思想

同样是一棵树，在bfs中我们要在所有分支中找到能够走的最远的那条路

Emphasis

注意递归时条件的判断

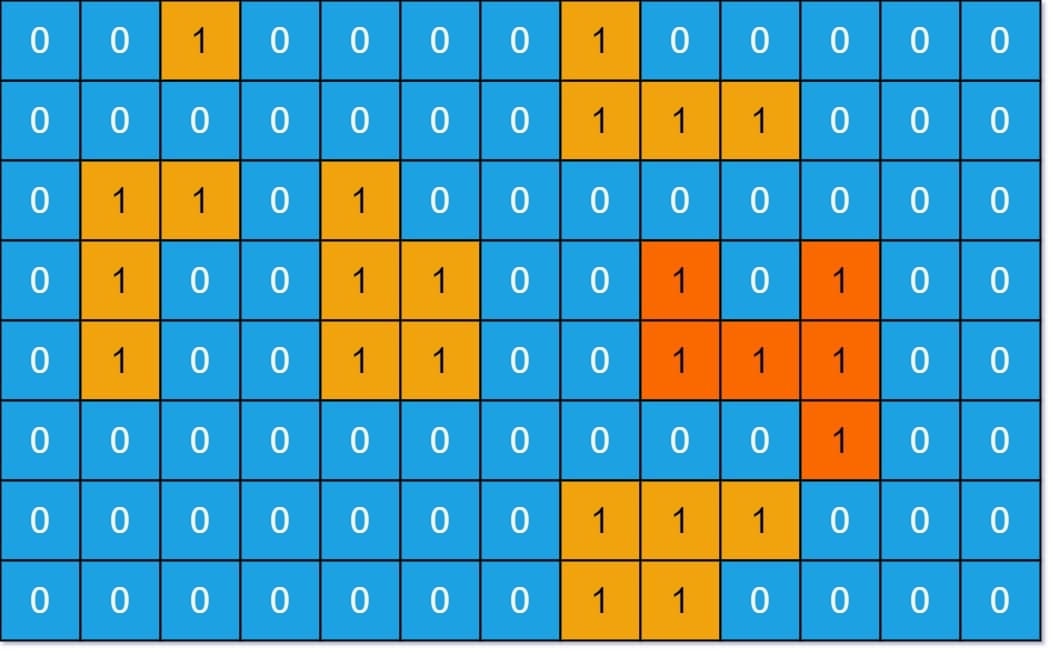
例题1

(此题来源于leetcode:https://leetcode-cn.com/problems/max-area-of-island/)

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直的四个方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

代码实现

class Solution {
    public int maxAreaOfIsland(int[][] grid) {
        int ans=0;
        for(int i=0;i<grid.length;i++){
            for(int j=0;j<grid[0].length;j++){
                ans=Math.max(ans,bfs(grid,i,j));
            }
        } 
        return ans;
    }

    int bfs(int[][] grid,int i,int j){
        if(i<0||i>=grid.length||j<0||j>=grid[0].length||grid[i][j]==0){
            return 0;
        }
        grid[i][j]=0;
    int count=1;
    count+=bfs(grid,i-1,j);
    count+=bfs(grid,i+1,j);
    count+=bfs(grid,i,j+1);
    count+=bfs(grid,i,j-1);
    return count;
    }
}

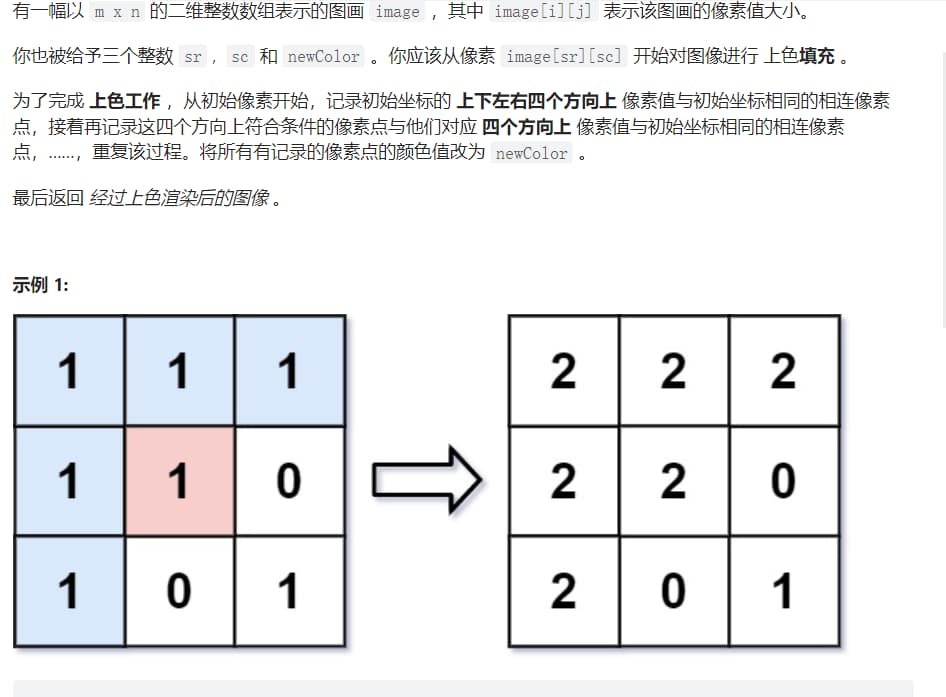
例题2

代码实现

class Solution {
    public int[][] floodFill(int[][] image, int sr, int sc, int newColor) {
        return dfs(image, sr, sc, newColor, image[sr][sc]);
    }

    public int[][] dfs(int[][] image, int i, int j, int newColor, int num){
        //1.坐标越界
        //2.当前坐标已经被染色
        //3.邻近坐标初始值与辐射坐标初始值不同
        if(i<0 || i>=image.length || j<0 || j>=image[0].length || image[i][j]==newColor || image[i][j]!=num){
        }else{
            int temp=image[i][j];
            image[i][j]=newColor;
            dfs(image, i+1, j, newColor, temp);
            dfs(image, i-1, j, newColor, temp);
            dfs(image, i, j+1, newColor, temp);
            dfs(image, i, j-1, newColor, temp);
        }
        return image;
    }
}

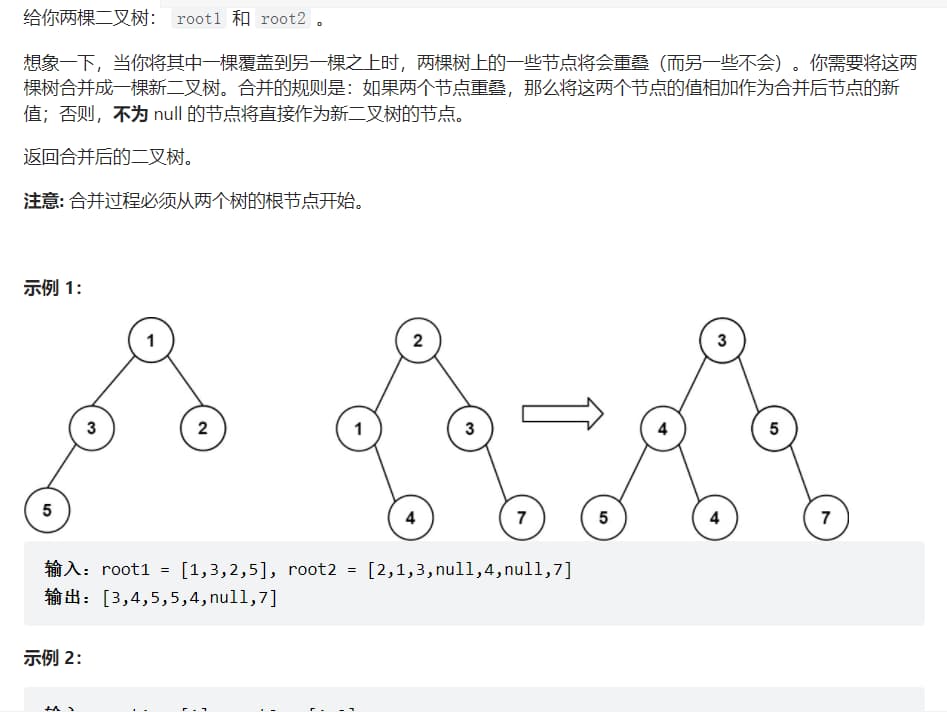
例题3

代码实现

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if(root1==null&&root2==null) return null;
        TreeNode root=new TreeNode((root1==null?0:root1.val)+(root2==null?0:root2.val));

        root.left=mergeTrees(root1==null?null:root1.left,root2==null?null:root2.left);
        root.right=mergeTrees(root1==null?null:root1.right,root2==null?null:root2.right);

        return root;
    }
}

算法Algorithm

基础算法

排序

快速排序

基本思想

Emphasis

具体实现

拓展题目

归并排序

基本思想

Emphasis

具体实现

拓展题目

二分查找

基本思想

Emphasis

具体实现

拓展题目

前缀和

基本思想

Emphasis

具体实现

拓展题目

差分

双指针

基本思想

Emphasis

具体实现

核心思想

拓展题目

位运算

基本思想

Emphasis

具体实现

拓展题目

拓展题目2:

离散化

基本思想

Emphasis

具体实现

例题：

区间合并

基本思想

Emphasis

具体实现

数据结构

单链表

结构特征

代码实现

数组版本

指针版本

双链表

结构特征

代码示例

数组版本

指针版本

栈

结构特征

代码实现

扩展题目

滑动窗口

结构特征

代码实现

KMP

算法特征

暴力写法

代码实现

Trie(字典树)

结构特征

代码实现

扩展题目

并查集

算法思想

基本原理

例题描述

代码实现

拓展题目

堆

结构特征

代码实现